三级毛片在线播放_三人性free欧美多人_三级爱草视频在线观看_日本三级黄线在线播放

　　有限元軟件一般提供兩種失穩分析方法，即特征值屈曲分析和非線性屈曲分析。上節兩個失穩實例是用特征值分析計算的。特征值法是彈性分析，不能用于出現塑性變形的結構。由于金屬膨脹節中波紋管的柱失穩和平面失穩都可能在塑性狀態下發生，因此本文采用了非線性屈曲分析，材料模型為彈性理想塑性體。本節算例假設材料的彈性模量為2*10^5mpa、屈服應力為230mpa。有限元軟件為ANSYS，采用SHell 51殼單元。進行非線性屈曲分析需要給波紋管設置初始缺陷，使其成為非軸對稱體。初始缺陷可以是波紋局部材料不均勻或形狀不規整。造成失穩的內壓用弧長法計算。
　　　　　
　　1.柱失穩
　　波紋管幾何參數：內徑150mm、波高25mm、波距25mm、壁厚0.5mm、10個波。用公式計算的內壓為0.17MPa（已加系數）。圖5和圖6是內壓為0.5Mpa時的彈性解。圖7是用弧長法求得的載荷-撓度曲線，圖中顯示內壓為0.69MPA（未加系數）——達到該值撓度劇增。圖8為屈曲時的形狀。
　　　　　
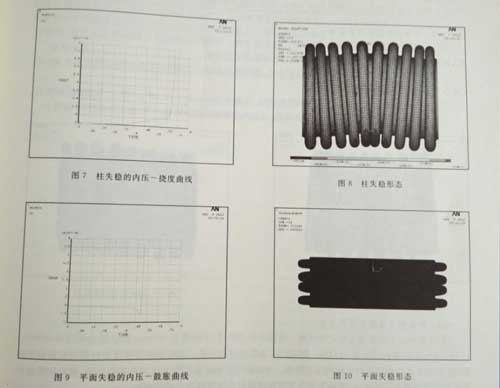
　　2.平面失穩
　　波紋管幾何參數：內徑300mm、波高30mm、波距30mm、壁厚0.8mm、4個波。用公式計算的內壓為0.63mpa（已加系數）。圖9位載荷——撓度曲線，圖中顯示內壓位1.05mpa（未加系數）。圖10為屈曲時的形狀。
　　3.小結
　　用非線性屈曲分析即可以得出柱失穩又可以得出平面失穩，從側面說明這兩種失穩機理相同，波紋管終發生何種失穩因波紋參數而定（主要是波數）。